Protéines et acides aminés??

 

http://fr.wikipedia.org/wiki/Repliement_de_prot%C3%A9ine

Le processus de repliement in vivo débute parfois lors de la traduction, c'est-à-dire que la terminaison N de la protéine commence à se replier alors que la portion terminale C de la protéine est toujours en cours de synthèse par le ribosome. Les protéines spécialisées appelées chaperonnes aident au repliement des autres protéines[8]. Le système bactérien GroEL, qui aide au repliement des protéines globulaires, est un exemple bien étudié. Dans les organismes eucaryotes, les protéines chaperonnes sont connues sous le nom de protéines de choc thermique. Bien que la plupart des protéines globulaires soient capables d'atteindre leur état natif sans assistance, les repliements assistés par les protéines chaperonnes sont parfois nécessaires dans un environnement intracellulaire encombré afin de prévenir l'agrégation ; les protéines chaperonnes sont aussi utilisées pour empêcher les mauvais repliements et les agrégations pouvant se produire en conséquence d'une exposition à la chaleur ou à d'autres changements dans l'environnement cellulaire.

Le point essentiel du repliement, cependant, reste que la séquence d'acides aminés de chaque protéine contient l'information spécifiant à la fois la structure native et le chemin pour y accéder. Ce qui ne veut pas dire que deux séquences d'acides aminés identiques se replient à l'identique. Les conformations diffèrent selon les facteurs environnementaux par exemple; des protéines similaires se replient différemment selon l'endroit où elles se trouvent. Le repliement est un processus spontané indépendant de l'apport énergétique des nucléosides triphosphates. Le passage à l'état replié est principalement guidé par les interactions hydrophobes, la formation de liaisons hydrogènes intramoléculaires et les forces de Van der Waals, et est contrarié par l'entropie conformationnelle, qui peut être surmontée par des facteurs extrinsèques comme les protéines chaperonnes.

Écart à l'état natif [modifier]

Dans certaines solutions et sous certaines conditions les protéines ne peuvent se replier dans leurs formes biochimiques fonctionnelles. Des températures au-dessus (et parfois en dessous) de l'intervalle dans lequel les cellules vivent causeront le non-repliement des protéines, ou leur dénaturation (c'est une des raisons pour lesquelles le blanc d'œuf est opaque après avoir bouilli). Des fortes concentrations de solutés, des valeurs de pH extrêmes, des forces mécaniques appliquées, ou encore la présence de dénaturants chimiques peuvent conduire au même résultat. Une protéine complètement dénaturée ne possède ni structure tertiaire ni structure secondaire, et existe sous forme de pelote aléatoire. Sous certaines conditions, certaines protéines peuvent se replier à nouveau ; cependant, dans de nombreux cas la dénaturation est irréversible[9]. Les cellules protègent parfois leurs protéines contre l'influence de la chaleur avec des enzymes connues sous le nom de chaperonnes ou protéines de choc thermique, qui aident les autres protéines à la fois à se replier et à rester pliées. Certaines protéines ne se replient jamais dans les cellules sans l'aide des protéines chaperonnes, qui sont en mesure d'isoler les protéines les unes des autres, ce qui fait que leur repliement n'est pas interrompu par les interactions avec les autres protéines. Elles peuvent aussi aider à déplier les protéines mal repliées, en leur donnant une autre chance de se replier correctement. Cette fonction est cruciale pour prévenir du risque de précipitation en agrégats amorphes insolubles.

En raison des plusieurs voies possibles de repliement, il peut exister plusieurs structures possibles. Une peptide constitué de seulement cinq acides aminés peut se replier en plus de 100 milliards de structures potentielles [15]. 

Techniques de détermination des structures de protéines [modifier]

La détermination de la structure repliée d'une protéine est une procédure longue et complexe, impliquant des méthodes comme la diffractométrie de rayons X ou la RMN. Un des champs de plus grand intérêt est la prédiction des structures natives à partir des seules séquences d'acides aminés en utilisant la bio-informatique et des méthodes de simulations numériques.

 

Le terme bioinformatics a été forgé en 1979 par Paulien Hogeweg de l'université d'Utrecht, Pays-Bas, conjointement avec Ben Hesper. La définition qu'ils lui ont donnée est la suivante : l'étude des procédés informatiques dans les systèmes biotiques.

Cela va de l'analyse du génome à la modélisation de l'évolution d'une population animale dans un environnement donné, en passant par la modélisation moléculaire, l'analyse d'image, le séquençage du génome et la reconstruction d'arbres phylogénétiques (phylogénie). Cette discipline constitue la « biologie in silico », par analogie avec in vitro ou in vivo.

  • La bioinformatique des séquences, qui traite de l'analyse de données issues de l'information génétique contenue dans la séquence de l'ADN ou dans celle des protéines qu'il code. Cette branche s'intéresse en particulier à l'identification des ressemblances entre les séquences, à l'identification des gènes ou de régions biologiquement pertinentes dans l'ADN ou dans les protéines, en se basant sur l'enchaînement ou séquence de leurs composants élémentaires (nucléotides, acides aminés).
  • La bioinformatique structurale, qui traite de la reconstruction, de la prédiction ou de l'analyse de la structure 3D ou du repliement des macromolécules biologiques (protéines, acides nucléiques), au moyen d'outils informatiques.
  • La bioinformatique des réseaux, qui s'intéresse aux interactions entre gènes, protéines, cellules, organismes, en essayant d'analyser et de modéliser les comportements collectifs d'ensembles de briques élémentaires du Vivant. Cette partie de la bioinformatique se nourrit en particulier des données issues de technologies d'analyse à haut débit comme la protéomique ou la transcriptomique pour analyser des flux génétiques ou métaboliques.
  • La bioinformatique statistique et la bioinformatique des populations

La bioinformatique est donc une branche théorique de la biologie[2].

http://fr.wikipedia.org/wiki/Alignement_de_s%C3%A9quences

Utilisation [modifier]

Dans la compréhension du fonctionnement de la vie, les protéines jouent un rôle essentiel. On part donc de l'hypothèse que des protéines comportant des séquences similaires risquent fort de posséder des propriétés physico-chimiques identiques. À partir de l'identification de similarités entre la séquence d'une première protéine dont on connaît le mécanisme d'action et celle d'une deuxième protéine dont on ne connaît pas le mécanisme de fonctionnement, on peut inférer des similarités structurelles ou fonctionnelles sur la séquence non connue et proposer de vérifier de manière expérimentale le comportement d'action supposé.

 

Alignements locaux et globaux

Global-local-alignment.pngLes alignements globaux sont plus souvent utilisés quand les séquences mises en jeu sont similaires et de taille égale. Une technique générale, appelée algorithme de Needleman-Wunsch est basée sur la programmation dynamique.

Les alignements locaux sont plus souvent utilisés quand deux séquences dissemblables sont soupçonnées de posséder des motifs semblables malgré l'environnement. L'algorithme de Smith-Waterman est une méthode d'alignement local générale basée aussi sur la programmation dynamique.

Avec des séquences suffisamment identiques, il n'y aucune différence dans les résultats.

Des méthodes hybrides, des méthodes semi-locales, s'avèrent utiles quand ...

 

Alignement par paire [modifier]

Les méthodes d'alignement par paires sont utilisées pour trouver les correspondances entre deux alignements de suites mais ne demandent pas une précision extrême.

 http://fr.wikipedia.org/wiki/Programmation_dynamique

La programmation dynamique est une technique algorithmique pour optimiser des sommes de fonctions monotones non décroissantes sous contrainte.

 Principe [modifier]

La programmation dynamique s'appuie sur un principe simple : toute solution optimale s'appuie elle-même sur des sous-problèmes résolus localement de façon optimale[1]. Concrètement, cela signifie que l'on va pouvoir déduire la solution optimale d'un problème en combinant des solutions optimales d'une série de sous problèmes. Les solutions des problèmes sont étudiées 'de bas en haut', c'est-à-dire qu'on calcule les solutions des sous-problèmes les plus petits pour ensuite déduire petit à petit les solutions de l'ensemble.

Par exemple pour optimiser la production de 30 puits à budget donné, on optimise la gestion de 2 puits pour tout budget inférieur ou égal[2], puis on considère l'ensemble comme un puits unique et on ajoute les puits suivants un par un.

Un autre exemple est le problème du sac à dos.

 

Algorithme génétique [modifier]

Exemple de l'évolution d'une population avec un algorithme génétique. Les objets sont ceux utilisés pour l'exemple de l'algorithme glouton. Par exemple, le génome (0,1,0,1,0) correspond à une sélection de la boîte de 12 kg et celle de 7 kg.

Les algorithmes génétiques sont souvent utilisés dans les problèmes d'optimisation difficiles comme celui du sac à dos. Ils sont relativement faciles à mettre en œuvre et permettent d'obtenir rapidement une solution satisfaisante même si la taille du problème est importante.

On génère une population d'individus dont les chromosomes symbolisent une solution du problème. La représentation d'un individu est binaire puisque chaque objet sera soit retenu, soit écarté du sac. Le nombre de bits dans le génome de chaque individu correspond au nombre d'objets disponibles.

L'optimisation suit les principes habituels de l'algorithme génétique. Les individus sont évalués puis les meilleurs sont retenus pour la reproduction. Selon l'évolution retenue, les opérateurs de reproduction peuvent être plus ou moins complexes (cross-over), des mutations peuvent également intervenir (remplacement d'un 0 par 1 ou l'inverse). On peut également décider de copier le meilleur individu pour la génération suivante (élitisme). Après un certain nombre de générations, la population tend vers un optimum, voire la solution exacte.

 

Utilisation pratique [modifier]

En pratique, la version multidimensionnelle peut servir à modéliser et résoudre le problème du remplissage d'un container dont le volume et la charge maximale sont limitées.

Un autre exemple est celui de la gestion de personnel. Dans une version simplifiée, on estime la productivité ou la compétence de chaque personne (son « poids » dans le problème), et on lui attribue d'autres variables : son coût et sa disponibilité. Chacun de ces paramètres représente une dimension du sac à dos. On définit finalement les contraintes liées à son projet eu égard les paramètres précédents : le budget disponible et le temps imparti pour réaliser le travail. La résolution permet de déterminer quelles personnes doivent être retenues pour réaliser le projet.

Sac à dos multi-objectif [modifier]

Une variante du problème consiste, à partir d'objets ayant plusieurs valeurs, à maximiser plusieurs fonctions objectifs, c'est le problème du sac à dos multi-objectif (MOKP). On rentre donc dans le domaine de l'optimisation multi-objectif.

Par exemple, supposons que vous lanciez une société spécialisée dans les croisières. Pour vous faire connaître, vous décidez d'inviter des gens célèbres à bord de votre plus beau bateau. Ce bateau ne peut supporter plus d'une tonne de passagers (ce sera la constante W). Chaque passager a une masse (wi), vous apporte de la publicité par sa popularité (pi1 : indice de popularité) et vous demande un salaire (pi2 : salaire négatif). Vous voulez, bien sûr, maximiser la publicité apportée et minimiser le salaire total à payer (maximiser le salaire négatif). De plus vous voulez avoir un maximum de gens sur votre bateau (pi3 = 1). Vous avez donc trois sommes à maximiser.

En termes mathématiques, vous cherchez le vecteur X de gens célèbres satisfaisant le problème :

  • max z^1(X) = \sum_{i=1}^n x_ip_i^1 : on veut une popularité maximale ;
  • max z^2(X) = \sum_{i=1}^n x_ip_i^2 : minimiser le salaire à payer (maximiser le salaire négatif) ;
  • max z^3(X) = \sum_{i=1}^n x_ip_i^3 : et avoir un maximum de gens sur le bateau

sous contraintes

  • \sum_{i=1}^n x_iw_i \le W : le bateau ne doit pas couler.

D'une manière générale, on remplace la fonction objectif du problème initial par une famille de fonctions objectifs :

  • max z^j(X) = \sum_{i=1}^n x_ip_i^j, \forall j \in \{1, \dots, m\}

Sac à dos quadratique [modifier]

Le problème de sac à dos quadratique est noté QKP. On a ici un gain gij supplémentaire lorsque deux objets (i et j) sont pris simultanément. Par exemple, disons que vous souhaitiez maximiser la qualité de votre café lors d'une expédition avec un sac à dos. On peut comprendre qu'il est plus intéressant d'apporter une cuillère et un sucre plutôt qu'un seul des deux.

La fonction objectif s'écrit alors :

  • max z(X) = \sum_{i=1}^n x_ip_i + \sum_{i=1}^n\sum_{j=1}^n x_ix_jg_{ij}

Problème de la somme de sous-ensembles ou du subset sum [modifier]

La particularité du problème de la somme de sous-ensembles (en anglais : subset sum) est que la valeur et le poids des objets sont identiques (pi = wi). C'est un problème important du domaine de la cryptographie, utilisé dans plusieurs systèmes de génération de clé publique.

Sac à dos à choix multiple [modifier]

Dans le problème de sac à dos à choix multiple (MCKP), les objets sont regroupés en classes, et il ne faut prendre qu'un seul représentant pour chaque classe.

Par exemple, vous êtes en train de confectionner votre boîte à outils. Si vous avez cinq clés à molette. Vous pouvez soit choisir la plus légère, afin de prendre un marteau performant, ou alors choisir la clé la plus performante et un marteau bas de gamme, ou alors faire un compromis. L'idée générale est que vous ne pouvez pas prendre plus d'une clé, ni plus d'un marteau.

Si les objets sont rangés en k classes, on notera N_j, j \in \{1,\dots, k\} l'ensemble des indices des objets appartenant à la classe j. On considère, bien entendu, qu'un objet n'appartient qu'à une unique classe. La formulation du problème devient :

 

  • max z(X) = \sum_{j=1}^k\sum_{i \in N_j} x_i^jp_i^j

sous contraintes :

  • \sum_{j=1}^k\sum_{i \in N_j} x_i^jw_i^j \le W : on ne dépasse pas la capacité du sac ;
  • \sum_{i \in N_j} x_i^j \le 1, \forall j \in \{1, \dots, k\} : on choisit au plus un représentant de chaque classe.

Sac à dos multiple [modifier]

Le problème de sac à dos multiple (MKP) consiste à répartir un ensemble d'objets dans plusieurs sacs à dos de capacités différentes. La valeur d'un objet dépend maintenant du sac dans lequel il est placé. Par exemple, on peut considérer qu'un euro a plus de valeur sur un compte d'épargne que sur un compte courant.

Si on a k sacs à dos, on notera 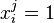x_i^j=1 si l'objet i est placé dans le sac j. La formulation du problème devient :

  • max z(X) = \sum_{j=1}^k\sum_{i=1}^n x_i^jp_i^j

sous contraintes

  • \sum_{i=1}^n x_i^jw_i \le W^j, \forall j \in \{1, \dots, k\} : on ne dépasse pas la capacité des sacs ;
  • \sum_{j=1}^k x_i^j \le 1, \forall i \in \{1, \dots, n\} : un objet n'est mis que dans un sac.

Il existe une variante de ce problème dans laquelle tous les sacs ont la même capacité, on le note MKP-I.

Suite !!

 

 

 

Créer un site internet avec e-monsite - Signaler un contenu illicite sur ce site

×