Conversion analogique-numérique [modifier]
Puisque les signaux naturels sont presque tous des signaux continus et que les circuits numériques ne manipulent que des données discrètes, il faut d'abord transformer ces signaux avant de pouvoir leur appliquer un traitement numérique. Cette transformation s'appelle la digitalisation ou numérisation ; elle est réalisée par un convertisseur analogique-numérique. Cette opération comprend deux actions :
L'échantillonnage transforme un signal continu 
en un signal discret 
composé de plusieurs mesures du signal continu, relevées à des instants successifs séparés par un pas temporel constant. Ainsi : 
où 
est la période d’échantillonnage. 
est la fréquence d’échantillonnage.
D’après le théorème d'échantillonnage de Nyquist-Shannon, un signal dont les composantes fréquentielles sont inférieures à 
est échantillonné de façon réversible : il est possible de reconstituer le signal continu à partir des valeurs discrètes. La fonction interpolante utilisée à cette fin est le sinus cardinal (noté sinc) :
De façon à éviter les artéfacts de « repliements de spectre », il est nécessaire d'éliminer les composantes fréquentielles au-delà de . Cela est réalisé par un filtre (analogique), appelé filtre anticrènelage, possédant en général une coupure raide (d'ordre élevé).
Un filtre calcule un signal discret 
à partir d’un signal discret 
. Chaque échantillon de est une combinaison linéaire d’échantillons de .
Un filtre est dit causal si l’échantillon ne dépend exclusivement que des valeurs de 
pour 
, c’est-à-dire des valeurs antérieures. C'est le cas de tous les systèmes réels, qui ne peuvent pas anticiper les valeurs futures. Toutefois, grâce à la mémorisation des signaux rendue possible par la numérisation, on peut réaliser des réponses impulsionnelles d'apparence non-causale.
Un filtre linéaire et invariant est caractérisé par sa réponse impulsionnelle, ie. la réponse à une entrée ne comportant qu’une valeur non nulle. La nature de cette réponse caractérise le filtre qui peut être à réponse impulsionnelle finie (RIF) ou infinie (RII). La sortie d’un filtre est la convolution de l’entrée par la réponse impulsionnelle. Cette convolution donne un algorithme de calcul d’un filtre RIF. Cette convolution peut être également calculée par transformée de Fourier rapide. Pour réaliser des filtres de type RII, on utilise des techniques récursives (la sortie du filtre dépend des échantillons de sortie précédents).
La transformée en Z de la réponse impulsionnelle est la fonction de transfert du filtre. Sa factorisation permet de décrire un filtrage par une équation aux différences discrètes. La transformée de Fourier — c'est-à-dire la transformée en Z pour 
— de la réponse impulsionnelle est la « réponse en fréquence » du filtre : elle permet de passer dans un domaine spectral.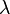 
est la fréquence réduite : 
.
Le calcul des coefficients d’un filtre pour obtenir une réponse en fréquence spécifiée est appelé « synthèse du filtre. »
Analyse spectrale [modifier]
La transformée de Fourier discrète (TFD) est utilisée pour calculer numériquement le spectre d'un signal, c’est-à-dire sa représentation fréquentielle. L’utilisation de cette TFD nécessite cependant quelques précautions. D’une part, parce qu’elle n’est applicable que sur un signal de durée limité : le signal doit donc souvent être tronqué, ce qui entraîne l’apparition d’ondulations parasites sur le spectre — elles peuvent être atténuées par les techniques d'apodisation. D’autre part, parce que le spectre obtenu est lui-aussi échantillonné, ce qui rend son interprétation plus difficile. Une interpolation de ce spectre peut être souhaitable.
Mise en œuvre [modifier]
Le traitement de signaux déjà numérisés peut se faire sur des ordinateurs d’usage général. Dans les applications de traitement en temps réel, des microprocesseurs spécialisés sont utilisés (DSP). Pour plus de rapidité, des fonctions spécifiques sont réalisées directement sous la forme de circuits intégrés (ASIC) ou implantées sur des composants en logique programmable (FPGA).